Answer:
The constraints are
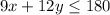

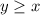
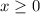
Explanation:
Let
x------> the number of visors
y------> the number of caps
we know that
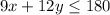 ----> inequality A
----> inequality A
 -----> inequality B
-----> inequality B
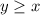 ----> inequality C
----> inequality C
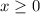 -----> inequality D (the number of caps can not be negative)
-----> inequality D (the number of caps can not be negative)
using a graphing tool
The solution is the shaded area
see the attached figure