Question

How to work it out logically? Question a !!!

Answer 1

2020.8 is the answer

Answer 2

Fencing is done along KL which is (1500+520.8=2020.8 m) from the top left corner and divides the property into half.

Explanation:

Given the figure with dimensions. we have to find the area of given figure.

Area of figure=ar(1)+ar(2)+ar(3)

Area of region 1 = ar(ANGI)+ar(AIB)

`=L* B+(1)/(2)* base* height\\\\=[1500* (5000-2000-1500)]+(1)/(2)* (3000-1500)* (5000-2000-1500)\\\\=3375000m^2=337.5ha`

Area of region 2 = ar(DHBC)

`=2000*1500\\\\=3000000m^2=300ha`

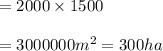
Area of region 3 = ar(GFEH)

`(2000+1500)* 1000\\\\=3500000m^2=350ha`

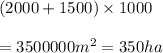
Hence, Area of figure=ar(1)+ar(2)+ar(3)=337.5ha+300ha+350ha

=987.5 ha

Now, we have to do straight-line fencing such that area become half and cost of fencing is minimum.

Let the fencing be done through x m downward from B which divides the two into equal area.

⇒ Area of upper part above fencing=Area of lower part below fencing

⇒
`ar(ANGB)+ar(GKLB)=ar(KLCM)+ar(MDCF)\\\\337500+3000x=(3500-x)* 1000+2000(1500-x)\\\\3375000+3000x=3500000-1000x+3000000-2000x\\\\6000x=315000\\\\x=(315000)/(6000)=520.8m`

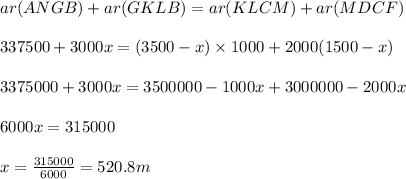
Hence, fencing is done along KL which is (1500+520.8=2020.8 m) from the top left corner and divides the property into half.