Answer:
Fencing is done along KL which is (1500+520.8=2020.8 m) from the top left corner and divides the property into half.
Explanation:
Given the figure with dimensions. we have to find the area of given figure.
Area of figure=ar(1)+ar(2)+ar(3)
Area of region 1 = ar(ANGI)+ar(AIB)
![=L* B+(1)/(2)* base* height\\\\=[1500* (5000-2000-1500)]+(1)/(2)* (3000-1500)* (5000-2000-1500)\\\\=3375000m^2=337.5ha](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4xralyislvarr0jvs4xjiz2e5p51munvd0.png)
Area of region 2 = ar(DHBC)
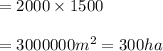
Area of region 3 = ar(GFEH)
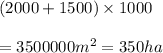
Hence, Area of figure=ar(1)+ar(2)+ar(3)=337.5ha+300ha+350ha
=987.5 ha
Now, we have to do straight-line fencing such that area become half and cost of fencing is minimum.
Let the fencing be done through x m downward from B which divides the two into equal area.
⇒ Area of upper part above fencing=Area of lower part below fencing
⇒
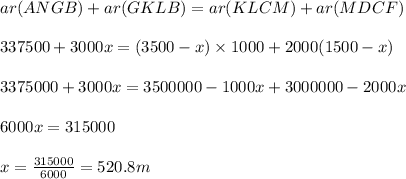
Hence, fencing is done along KL which is (1500+520.8=2020.8 m) from the top left corner and divides the property into half.