Question

n ΔDEF, DE = 11, EF = 9, and angle E = 140°. Which equation correctly uses the law of cosines to solve for the third side?

Answer 1

e2 = 112 + 92 − 2(11)(9)cos(140°)

i did the assignment i hope this helps some! :)

Explanation:

Triangle D E F is shown. Angle D E F is 140 degrees. The length of D E is 11, the length of E F is 9, and the length of D F is e.

In ΔDEF, DE = 11, EF = 9, and angle E = 140°.

Which equation correctly uses the law of cosines to solve for the third side?

e2 = 112 + 92 − 2(11)(9)cos(140°)

112 = e2 + 92 − 2e(9)cos(140°)

92 = e2 + 112 − 2e(11)cos(140°)

e = 11 + 9 − 2(11)(9)cos(140°)

Answer 2

`e^2=11^2+9^2-2*11*9*cos(140^o)`

Step-by-step explanation:

Please find the attachment.

We have been given that in ΔDEF, DE = 11, EF = 9, and angle E = 140°. We are asked to determine the equation that can be used to find the length of third side using law of cosines.

We can use Law of cosines to solve for a side of triangle, when we are given other two sides of the triangle and angle corresponding the side we need to figure out.

`c^2=a^2+b^2-2ac*cos(c)`

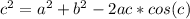
We can see from our attachment that e is side corresponding to angle 140 degrees, so to find the length of we can set an equation as:

`e^2=f^2+d^2-2fd*cos(e)`

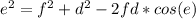
Upon substituting our given values we will get,

`e^2=11^2+9^2-2*11*9*cos(140^o)`

Therefore, the equation
`e^2=11^2+9^2-2*11*9*cos(140^o)` can be used to find the length of third side.

Let us solve for third side.

`e^2=121+81-198*cos(140^o)`

`e^2=121+81-198*(-0.766044443119)`

`e^2=121+81+151.676799737562`

`e^2=353.676799737562`

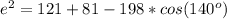
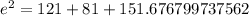
Let us take square root of both sides of our equation.

`e=√(353.676799737562)`

`e=18.806\approx 18.81`

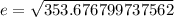
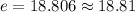
Therefore, the length of 3rd side of triangle DEF is 18.81.