Question

If a and b are integers whose product is 5, what is the least possible value of a^b? Someone please help

Answer 1

Answer: The answer is -1.

Step-by-step explanation: Given that 'a' and 'b' are integers such that their product is 5. We are to find the least possible value of 'a to the power b'.

Since a and b are integers and a × b = 5, so their possible values are

`a=1,~b=5,\\\\a=-1~b=-5,\\\\a=5,~b=1,\\\\a=-5,~b=-1.`

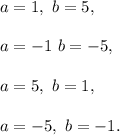
For these only four choices of a and b, we have the following values of a to the power b:

`a^b=1^5=1,\\\\a^b=(-1)^(-5)=(1)/((-1)^5)=(1)/(-1)=-1,\\\\\\a^b=5^1=5,\\\\a^b=(-5)^(-1)=(1)/((-5)^1)=-(1)/(5).`

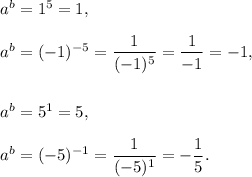
since -1 is the smallest among these four values, so the least possible value of 'a to the power b' is -1.

Thus, the answer is -1.