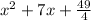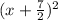Answer:

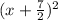
Explanation:
We always divide by 2 to the number in front of second term of the trinomial [ that is term with x ]
and then we add the square of such obtained number in order to make it perfect
therefore here number with second term is 7 ,Dividing 7 by 2 ,we get
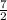
on squaring it we get
therefore here number with second term is 7 ,Dividing 7 by 2 ,we get

So expression is