Answer:
Measure of ∠ADC = 22.62°
Explanation:
Firstly, we have right triangle ABC with AB = 12 cm and BC = 5 cm.
'Pythagoras Theorem' states that 'The sum of squares of the length of the sides in a right triangle is equal to the square of the length of the hypotenuse'.
That is,
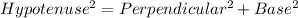
i.e.
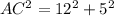
i.e.
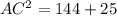
i.e.
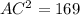
i.e.
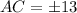
As, the length of the hypotenuse cannot be negative.
So, we get, AC = 13 cm.
Further, we have a right triangle ACD with perpendicular = AC = 13 cm and hypotenuse = AD = 33.8 cm.
As we know, 'In a right angled triangle, the angles and sides can be written in trigonometric forms'.
That is,
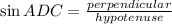
i.e.
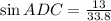
i.e.
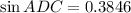
i.e.
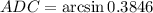
i.e.
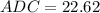
Thus, the measure of ∠ADC = 22.62°