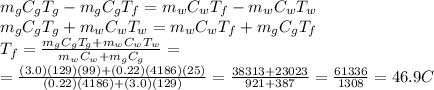Question

What is the final temperature when a 3.0 kg gold bar at 99 0C is dropped into 0.22 kg of water at 25oC?

Answer 1

`T_(f)=46.9C`

Step-by-step explanation:

Given:

`m_(g) =3.0kg`
`m_(w) =0.22kg`

`T_(g)=99 C`
`T_(w)=25C`

`c_(p,g)=129J/kg.C`
`c_(p,w)=4186J/kg.C`

Unkown:

`T_f=?`

Formula:

`T_f=(m_g.c_(p,g).T_g+m_w.c_(p,w).T_w)/(m_w.c_(p,w)+m_g.c_(p,g))`

Step by step solution:

`T_f=((3)(129)(99)+(0.22)(4186)(25))/((0.22)(4186)+(3)(129))`

`T_f=(61336)/(1308)`

`T_f=46.9C`

Answer 2

46.9 C

Step-by-step explanation:

The heat released by the gold bar is equal to the heat absorbed by the water:

`m_g C_g (T_g-T_f)=m_w C_w (T_f-T_w)`

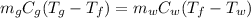
where:

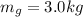`m_g = 3.0 kg` is the mass of the gold bar

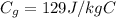`C_g=129 J/kg C` is the specific heat of gold

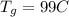`T_g=99 C` is the initial temperature of the gold bar

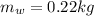`m_w = 0.22 kg` is the mass of the water

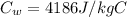`C_w=4186 J/kg C` is the specific heat of water

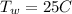`T_w=25 C` is the initial temperature of the water

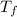`T_f` is the final temperature of both gold and water at equilibrium

We can re-arrange the formula and solve for T_f, so we find:

`m_g C_g T_g -m_g C_g T_f = m_w C_w T_f - m_w C_w T_w\\m_g C_g T_g +m_w C_w T_w= m_w C_w T_f +m_g C_g T_f \\T_f=(m_g C_g T_g +m_w C_w T_w)/(m_w C_w + m_g C_g)=\\=((3.0)(129)(99)+(0.22)(4186)(25))/((0.22)(4186)+(3.0)(129))=(38313+23023)/(921+387)=(61336)/(1308)=46.9 C`