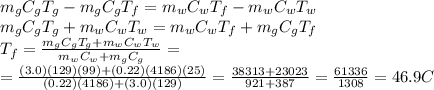Answer:
46.9 C
Step-by-step explanation:
The heat released by the gold bar is equal to the heat absorbed by the water:
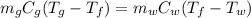
where:
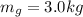 is the mass of the gold bar
is the mass of the gold bar
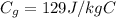 is the specific heat of gold
is the specific heat of gold
 is the initial temperature of the gold bar
is the initial temperature of the gold bar
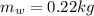 is the mass of the water
is the mass of the water
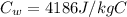 is the specific heat of water
is the specific heat of water
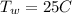 is the initial temperature of the water
is the initial temperature of the water
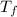 is the final temperature of both gold and water at equilibrium
is the final temperature of both gold and water at equilibrium
We can re-arrange the formula and solve for T_f, so we find: