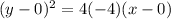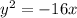Answer:
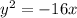
Explanation:
we know that
The equation of a horizontal parabola written in standard form is equal to
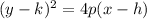
where
(h,k) is the vertex of the parabola
In this problem we have
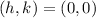
The coordinates of the focus are (h+p,k)
In this problem we have
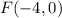
therefore
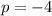
substitute