Question

What’s the answer to this please?

Answer 1

ANSWER

C. Yes, their slopes have product -1

Step-by-step explanation

The slope of the line connecting

P(1,3) and Q(7,8) is



`= (8 - 3)/(7 - 1)`


`= (5)/(6)`

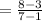
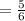
The slope of the line connecting
R(5,-7) and S(10,-13) is


`= ( - 13 - - 7)/(10 - 5)`



`= - (6)/(5)`


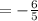
Product of the two slopes is


`= (5)/(6) * - (6)/(5)`


`= - 1`


Since the product is -1, the slopes are perpendicular.


The correct answer is C.