Question

A blimp provides aerial television views of a tennis game. The television camera sights the stadium at a 17degrees angle of depression. The altitude of the blimp is 400m. What is the​ line-of-sight distance from the television camera to the base of the stadium​? Round to the nearest hundred meters.

Answer 1

1379.31meters is the​ line-of-sight distance from the television camera to the base of the stadium​ .

Explanation:

As given

A blimp provides aerial television views of a tennis game.

The television camera sights the stadium at a 17degrees angle of depression. The altitude of the blimp is 400m.

Now by using the trignometric identity .

`sin\theta = (Perpendicular)/(Hypotenuse)`

As the figure is given below .

Perpendicular = AC = 400 m

Hypotenuse = AB

`\theta = 17^(\circ)`

Putting all the values in the identity .

`sin17^(\circ) = (400)/(AB)`

`0.29\ (Approx)= (400)/(AB)`

`AB= (400)/(0.29)`

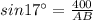
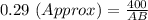
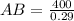
AB = 1379.31 meters

Therefore the 1379.31 meters is the​ line-of-sight distance from the television camera to the base of the stadium​ .