Question

A boat is 20 ft away from a point perpendicular to the shoreline. A person stands at a point down the shoreline so that a 60° angle is formed between the closest point to the boat, the person, and the boat. How far is the person from the boat? Draw a picture showing the right triangle. Round your answer to the nearest tenth of a foot. Show your work.

Answer 1

23.09 feet.

Explanation:

Please find the attachment.

Let x be the distance between the person and the boat.

We have been given that a boat is 20 ft away from a point perpendicular to the shoreline. A person stands at a point down the shoreline so that a 60° angle is formed between the closest point to the boat, the person, and the boat.

We can see from our attachment that the boat, shoreline and position of person forms a right triangle, where side with 20 feet length is opposite side and x is hypotenuse for our given angle.

Since we know that Sine relates the opposite and hypotenuse of a right triangle, so we will use Sine to find the value of x.

`\text{Sine}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

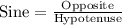
Upon substituting our given values in above formula we will get,

`\text{Sin}(60)=(20)/(x)`

`x=\frac{20}{\text{Sin}(60)}`

`x=(20)/(0.866025403784)`

`x=23.094\approx 23.09`

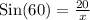
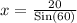
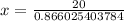
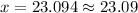
Therefore, the person is 23.09 feet away from the boat.