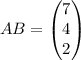Answer:
The product of given matrix is
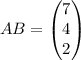
Explanation:
Given : Two matrix
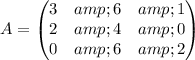
and
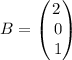
We have to find the product of given matrix
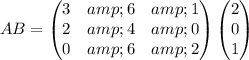
Multiply the rows of first matrix by the columns of second matrix , we have,
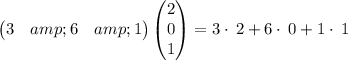
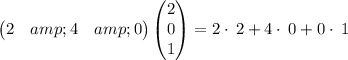
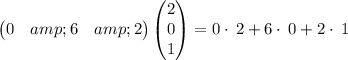
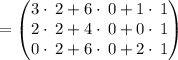
On , simplifying , we get,
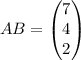
Thus, the product of given matrix is