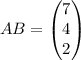Question

What is the product

Answer 1

Answer: The product is
`\left[\begin{array}{ccc}7\\4\\2\end{array}\right]`

Explanation:

Since we have given that

`\left[\begin{array}{ccc}3&6&1\\2&4&0\\0&6&2\end{array}\right] * \left[\begin{array}{ccc}2\\0\\1\end{array}\right]`

As we know the way to multiply in case of matrices.

Since the order of first matrix is 3×3

And the order of second matrix is 3 × 1

So, the order of the product matrix is 3 × 1

So, the product becomes

`\left[\begin{array}{ccc}3&6&1\\2&4&0\\0&6&2\end{array}\right] * \left[\begin{array}{ccc}2\\0\\1\end{array}\right]\\\\=\left[\begin{array}{ccc}3* 2+6* 0+1* 1\\2* 2+4* 0+0* 1\\0* 2+6* 0+2* 1\end{array}\right] \\\\=\left[\begin{array}{ccc}7\\4\\2\end{array}\right]`

Hence, the product is
`\left[\begin{array}{ccc}7\\4\\2\end{array}\right]`

Answer 2

The product of given matrix is
`AB=\begin{pmatrix}7\\ 4\\ 2\end{pmatrix}`

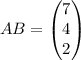
Explanation:

Given : Two matrix

`A=\begin{pmatrix}3&6&1\\ 2&4&0\\ 0&6&2\end{pmatrix}`

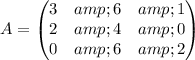
and
`B=\begin{pmatrix}2\\ \:0\\ \:1\end{pmatrix}`

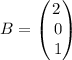
We have to find the product of given matrix

`AB=\begin{pmatrix}3&6&1\\ 2&4&0\\ 0&6&2\end{pmatrix}\begin{pmatrix}2\\ 0\\ 1\end{pmatrix}`

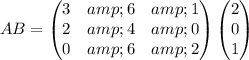
Multiply the rows of first matrix by the columns of second matrix , we have,

`\begin{pmatrix}3&6&1\end{pmatrix}\begin{pmatrix}2\\ 0\\ 1\end{pmatrix}=3\cdot \:2+6\cdot \:0+1\cdot \:1`

`\begin{pmatrix}2&4&0\end{pmatrix}\begin{pmatrix}2\\ 0\\ 1\end{pmatrix}=2\cdot \:2+4\cdot \:0+0\cdot \:1`

`\begin{pmatrix}0&6&2\end{pmatrix}\begin{pmatrix}2\\ 0\\ 1\end{pmatrix}=0\cdot \:2+6\cdot \:0+2\cdot \:1`

`=\begin{pmatrix}3\cdot \:2+6\cdot \:0+1\cdot \:1\\ 2\cdot \:2+4\cdot \:0+0\cdot \:1\\ 0\cdot \:2+6\cdot \:0+2\cdot \:1\end{pmatrix}`

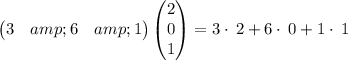
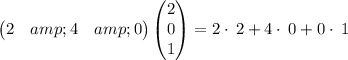
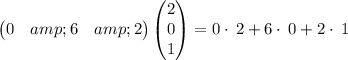
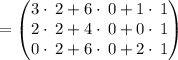
On , simplifying , we get,

`AB=\begin{pmatrix}7\\ 4\\ 2\end{pmatrix}`

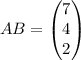
Thus, the product of given matrix is
`AB=\begin{pmatrix}7\\ 4\\ 2\end{pmatrix}`