Answer:
(D) 16
Explanation:
It is given that Segment EA is an altitude of triangle DEF. Point D(-2,1), E(2,5), F(6,1) and A(2,1).
Now, using the distance formula, we have
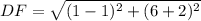
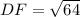
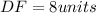
And
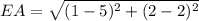
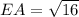
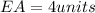
Thus, the area of the triangle is=
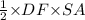
=
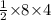
=

Thus, the area of the triangle is 16 sq units.