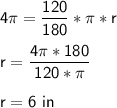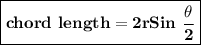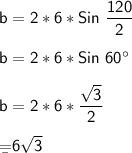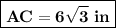Answer:
AC = 6√3 in
Explanation:
Finding the length of the chord:
Join OC. Now ΔAOC is an isosceles triangle as OA = OC =radius.
∠A = ∠C = 30.
∠A + ∠C + ∠AOC = 180 {angle sum property of traingle}
30 + 30 + ∠AOC = 180°
∠AOC = 180 -60
∠AOC = Ф = 120°
Find the length of radius using the bellow formula.
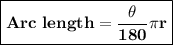
Ф = 120°
Arc length = 4π