Answer:
Option A is correct. since series is convergent.
Step-by-step explanation
nth term of the given series is given by
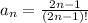
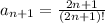

on simplifying it ,we get
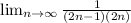
which gives zero at n = infinity
since value of the limit of the ratio is less than 1
given series is convergent [ by ratio test ]