Question

in 18.6 kg person climbs up a uniform ladder with negligible mass. the upper end of the ladder rest on a frictionless wall. the bottom of the ladder rest on a floor with a rough surface where the coefficient of static friction is 0.63. the angle between the horizontal and the ladder is theta. the person wants to climb up the ladder a distance of 1.6m along the ladder from the ladders foot. what is the minimum angle so that the person can reach the distance of 1.6m without having the ladder slip?

Answer 1

The minimum angle required for the person to get to as distance of 1.6 m is

57.9°

• The normal force can be separated into vertical and horizontal. Then to calculate the normal force we use

`Normal force= (m*g)= (18.6*9.8)=182.3N`

• The horizontal force, which is the floor frictional force can be gotten

F= (∪
`N)`

`=(0.63*182.3)=114.8N`

• We can calculate the minimum angle using this formula

(F*tan θ
`= mg`)

F= floor frictional force= 114.7N

m= 18.6 kg

• Then substitute, we have

[114.7*tan θ)
`=(18.6*9.81)]`

114.7*tan θ =
`(182.5)/(114.7)`

`=57.9`°

Therefore, the minimum angle is =57.9°

Answer 2

let the normal force due to vertical wall is N1 and due to horizontal floor is N2

now by force balance we can say

`N2 = mg`

`N_2 = 18.6(9.8) = 182.3 N`

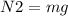
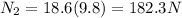
now friction force on the floor is given as

`F_f = \mu N`

`F_f = 0.63(182.3) = 114.8 N`

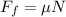
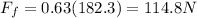
now by torque balance we will have

torque due to normal of vertical wall = torque due to weight of man

so here we have

`N_1 (Lsin\theta) = mg(Lcos\theta)`

`N_1 tan\theta = mg`

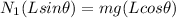
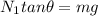
also we know that

`N_1 = F_f = 114.8 N`

`114.8 tan\theta = 18.6(9.8)`

`\theta = 57.8 degree`

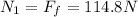
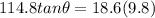
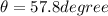
so above is the angle with the floor