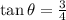Question

Find the exact values of a) sec of theta b)tan of theta if cos of theta= -4/5 and sin<0

Answer 1

Using trigonometric ratio:

`\sec \theta = (1)/(\cos \theta)`

`\tan \theta = (\sin \theta)/(\cos \theta)`

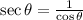
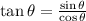
From the given statement:

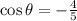`\cos \theta = -(4)/(5)` and sin < 0

⇒
`\theta` lies in the 3rd quadrant.

then;

`\sec \theta = (1)/(-(4)/(5)) = -(5)/(4)`

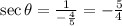
Using trigonometry identities:

`\sin \theta = \pm √(1-\cos^2 \theta)`

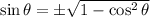
Substitute the given values we have;

`\sin \theta = \pm\sqrt{1-((-4)/(5))^2 } =\pm\sqrt{1-(16)/(25)} =\pm\sqrt{(25-16)/(25)} =\pm \sqrt{(9)/(25) } = \pm(3)/(5)`

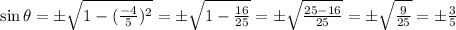
Since, sin < 0

⇒
`\sin \theta = -(3)/(5)`

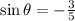
now, find
`\tan \theta`:

`\tan \theta = (\sin \theta)/(\cos \theta)`

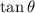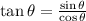
Substitute the given values we have;

`\tan \theta = (-(3)/(5) )/(-(4)/(5) ) = (3)/(5)* (5)/(4) = (3)/(4)`

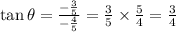
Therefore, the exact value of:

(a)

`\sec \theta =-(5)/(4)`

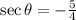
(b)

`\tan \theta= (3)/(4)`