Question

Given:
TB and TC are tangents to circle O
Prove:
TO is the bisector of ∠BTC.

Answer 1

Explanation:

Please find the attachment.

We have been given a circle and we are asked to prove that TO is the bisector of angle BTC.

To prove that TO is bisector of angle BTC, we just need to prove that angle BTO is congruent to angle CTO.

We have been given that TB and Tc are tangents to circle O. Since we know that tangents that meet at same point are equal in length.

`TB=TC\text{ ...By two-tangent theorem}`

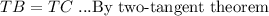
Since O is the center of our given circle, so OB and OC will be the radii of our given circle.

Since all the points on a circle are equidistant from the center and radius of circle has one one endpoint on the circle and one at the center, so all radii of a circle are congruent.

`OB=OC`

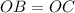
We also know that a tangent to a circle is perpendicular to the radius drawn to the point of tangency. As OB and OC are radii and TB and TC are tangents of our given circle,

`m\angle TBO=90^o`

`m\angle TCO=90^o`

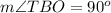
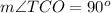
We can see in our triangles TBO and TCO that,

`TB=TC`

`m\angle TBO=m\angle TCO`

`OB=OC`

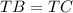
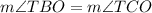
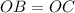
Therefore, by SAS congruence
`\Delta TBO\cong \Delta TCO`.

So by corresponding parts of congruent triangles are congruent
`\angle BTO\cong \angle CTO`, therefore, TO is the bisector of
`\angle BTC`.