Answer:
James will pay off his mortgage 136 months early.
Explanation:
Given : Amount to be paid(A)= $205000
Interest rate per annum = 5.78% = 0.0578
monthly interest rate(i) =
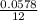 = 0.004817 (approx)
= 0.004817 (approx)
Monthly payment (P) = $1500.
we have to find how many months early will he pay off his mortgage
We know,
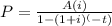
Substitute values , we get,
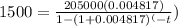
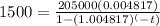
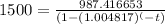
Solving for t ,
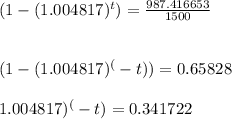
Applying ln both sides,we get,
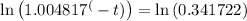
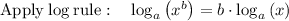
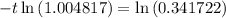
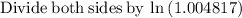
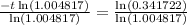
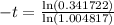
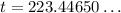
Thus, t = 224 months.
1 year = 12 month thus, 30 years = 360 months.
Difference = 360 - 224 = 136 months
Thus, James will pay off his mortgage (360-224) 136 months early.