Question

Which sum or difference identity would you use to verify that cos (180° - ∅) = -cos ∅?

a.
sin (α -β) = sin α cos β – cos α sin β
b.
cos (α -β) = cos α cos β – sin α sin β
c.
cos (α -β) = cos α cos β + sin α sin β
d.
sin (α + β) = sin α cos β + cos α sin β

Answer 1

Option (b) is correct.

b)
`\cos (\alpha-\beta)=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta`

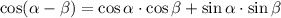
Explanation:

Given
`\cos (180^(\circ)-\phi)=-\cos \phi`

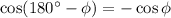
To prove the above stated formula we have to choose one of the identity from the given options .

Since right side of above formula is
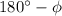`180^(\circ)-\phi` which is same as
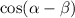`\cos (\alpha-\beta)`, we will use the identity
`\cos (\alpha-\beta)`

`\cos (\alpha-\beta)=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta`

`\cos (180^(\circ)-\phi)=\cos 180^(\circ)\cdot\cos\phi+\sin 180^(\circ)\cdot\sin\phi`

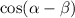
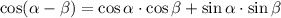
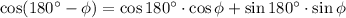
We know
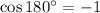`\cos 180^(\circ)=-1` and
`\sin 180^(\circ)=0`

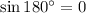
Substitute above, we get,

`\cos (180^(\circ)-\phi)=-\cos \phi`

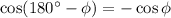
Thus, Option (b) is correct.

Answer 2

Answer: Option C is correct

Explanation:

We know tha tCos(A-B) = cosA cosB + sinAsinB

Plugging A = 180 and B = Ф

cos(180-Ф)= cos180cosФ+sin180sinФ

= (-1) cosФ+ (0) sinФ [ since cos180=-1 and sin180 =0]

= -cosФ + 0

= -cosФ

Therefore option C is the correct answer.