Answer: 1) After 17.673 years ( Approx) the population will be doubled.
2) After 53.019 years the population will be 80.
Explanation:
1) Let x represents the number of years after which the population will doubled,
Since rate of interest = 4%
And, initial number of fish = 10,
Hence the fish after x years =
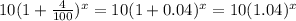
⇒

⇒
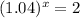
⇒
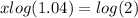
⇒

Hence, After 17.673 years ( Approx) the population will be doubled.
2) Let after y years the population will be 80.
⇒
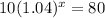
⇒
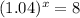
⇒

⇒
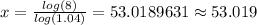
Hence, After 53.019 years the population will be 80.