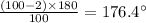Answer with Step-by-step explanation:
Regular polygon: That polygon in which all angles are equal in measure.
Measure of interior angles of polygon=
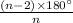
Where n=Number of sides
1.Triangle:Number of sides=3
Measure of each interior angle=

2.Quadrilateral:Number of sides=4
Measure of each interior angle=

3.Pentagon:Number of sides=5
Measure of each interior angle=
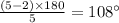
4.Octagon:Number of sides =8
Measure of each interior angle=
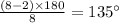
5.
Number of sides of decagon=10
Measure of each interior angle=
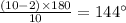
6.30-gon: Number of sides=30
Measure of each interior angle=
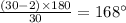
7.50-gon: Number of sides=50
Measure of each interior angle=
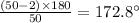
8.100-gon:
Number of sides=100
Measure of each interior angle=