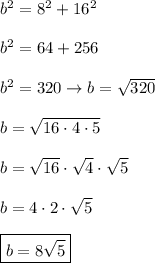Question

How to solve for a, b and f

Answer 1

`\large\boxed{a=4\sqrt5,\ b=8\sqrt5,\ f=8}`

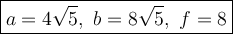
Explanation:

ΔBDC and ΔCDA are similar (AA). Therefore the sides are in proportion:

`(BD)/(DC)=(DC)/(DA)`

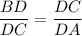
We have:

BD = 4, DA = 16 and DC = f. Substitute:

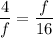`(4)/(f)=(f)/(16)` cross multiply

`f^2=(4)(16)\\\\f^2=64\to f=√(64)\\\\\boxed{f=8}`

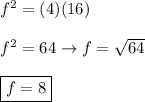
We can use the Pythagorean theorem:

`leg^2+leg^2=hypotenuse^2`

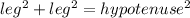
ΔBDC:

leg = 4, leg = 8, hypotenuse = a. Substitute:

`a^2=4^2+8^2\\\\a^2=16+64\\\\a^2=80\to a=√(80)\\\\a=√(16\cdot5)\\\\a=√(16)\cdot\sqrt5\\\\\boxed{a=4\sqrt5}`

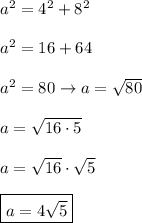
ΔCDA:

leg = 8, leg = 16, hypotenuse = b. Substitute:

`b^2=8^2+16^2\\\\b^2=64+256\\\\b^2=320\to b=√(320)\\\\b=√(16\cdot4\cdot5)\\\\b=√(16)\cdot\sqrt4\cdot\sqrt5\\\\b=4\cdot2\cdot\sqrt5\\\\\boxed{b=8\sqrt5}`