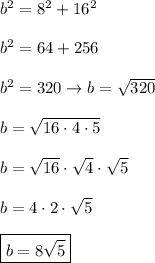Answer:
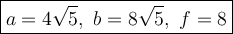
Explanation:
ΔBDC and ΔCDA are similar (AA). Therefore the sides are in proportion:
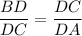
We have:
BD = 4, DA = 16 and DC = f. Substitute:
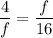 cross multiply
cross multiply
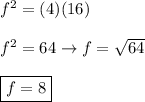
We can use the Pythagorean theorem:
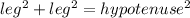
ΔBDC:
leg = 4, leg = 8, hypotenuse = a. Substitute:
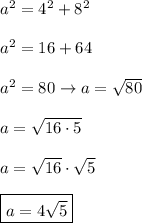
ΔCDA:
leg = 8, leg = 16, hypotenuse = b. Substitute: