Answer:
24
Explanation:
We are given the logarithmic expression:
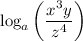
We are also given by the problem that:
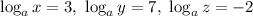
From the expression, we will simplify it using two properties:
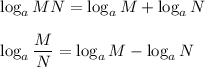
Therefore, apply the properties to simplify:
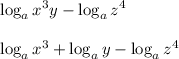
Next, we will use another property to take an exponent as a coefficient:
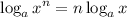
Hence:
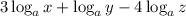
Substitute what are given in the problem and the answer will be:
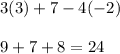
Hence, the answer is 24.