Question

For the quadratic function
`y=(x+4)^2-1` , do the following: a) rewrite the function in the standard form, b) rewrite the function in intercept form, c) find the vertex, d) find the y-intercept, e) find the x-intercepts.

Answer 1

`y=x^2+8x+15`

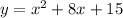
Intercept form is y= (x+5)(x+3)

vertex is (-4,1)

y intercept is (0,15)

x intercepts are (-5,0) (-3,0)

Explanation:

Given quadratic function

`y=(x+4)^2-1`

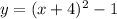
To rewrite it in standard form we need to expand (x+4)^2

`y=(x+4)(x+4)-1`

`y=x^2+8x+16-1`

`y=x^2+8x+15`

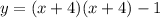
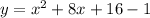
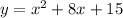
Intercept form is y=a(x-p)(x-q)

Factor x^2 + 8x + 15

product is 15 and sum is 8, 5*3= 15 and 5+3=8

(x+5)(x+3)

Intercept form is y= (x+5)(x+3)

Vertex form of equation is y=(x-h)^2+k

where (h,k) is the vertex

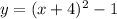`y=(x+4)^2-1`, here h = -4 and k =1 so vertex is (-4,1)

To find y intercept plug in 0 for x

y= (x+5)(x+3)

y= (0+5)(0+3) = 15, so y intercept is (0,15)

to find x intercept plug in 0 for y

y= (x+5)(x+3)

0= (x+5)(x+3), x+5 =0 and x+3=0

x=-5 and x= -3

So x intercepts are (-5,0) (-3,0)