Question

Estimate the area under the curve f(x) = 16 - x^2 from x = 0 to x = 3 by using three inscribed (under the curve) rectangles. Answer to the nearest integer.

Answer 1

43

Explanation:

Estimate the area under the curve f(x) = 16 - x^2 from x = 0 to x = 3 by using three inscribed (under the curve) rectangles

First we find out the width of the rectangle

Δx=b−a/n, a= 0 and b= 3, n= 3

so Δx= 1

Divide the interval [0,3] into 3 sub intervals of width=1

[0,1] [1,2] [2,3]

Now we plug in end point and evaluate the function

We take left endpoints

`f(x) = 16 - x^2`

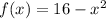
f(0) = 16 - 0^2=16

f(1) = 16 - 1^2= 15

f(2) = 16 - 2^2= 12

Now sum = Δx(f(0) + f(1)+f(2))

= 1 (16+15+12)= 43