Question

What is the similarity ratio of a cube with volume 729m^3 to a cube with volume 3375 m^3

Answer 1

The similitary ratio is 3:5

Explanation:

To answer this question let's call:

`V_1 = 729\ m^3` to volume 1.

Let's call:

`V_2 = 3375\ m^3` to volume 2

The relation k of simiiltud between both volumes we find dividing
`V_1` between
`V_2`

`(V_1)/(V_2) = k^3\\\\(V_1)/(V_2) = (729m^3)/(3375m^3)\\\\(V_1)/(V_2) = (27)/(125)\\\\(V_1)/(V_2) = (3^3)/(5^3)\\\\k^3 = ((3)/(5))^3\\\\k = (3)/(5)`

Answer 2

3/5

Explanation:

We are to find the similarity ratio of a cube with volume
`729 m^3` to a cube with volume
`3375 m^3`.

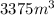We know the formula for the ratio of two cubes:

`(V_1)/(V_2) =k^3`

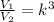
where
`k` is the similarity ratio of the two cubes.

Substituting the given values in the formula to find
`k`:

`k^3 = \frac {729} {3375}`

`k^3 = \frac {27} {125}`

`k^3 = (\frac {27} {125})^3`

`k=(3)/(5)`

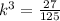
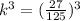
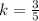
Therefore, the similarity ratio of the two cubes is 3/5.