Question

Find the maximum value of P= 4x + 5y
Subject to the following constraints :

Answer 1

Answer: The maximum value of P is 38 at (7,2)

Explanation:

To find the maximum value of
`P=4x+5y`

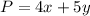
Subject to the following constraints:-

`x+3y\leq13\\3x+2y\leq25\\x\leq0,y\leq0`

From this we get boundary equations of the given inequalities as

`x+3y=13...........(1)\\3x+2y=25....................(2)\\x=0,y=0`

Now, find points from which the above lines are passing.

In (1) at y=0, x=13

At y=1, x=10

So line (1) passing through (13,0) and (10,1)

Similarly, In (2), at x=1, y=11

At y=2, x=7

So line (2) is passing through (1,11) and (7,2)

Plot theses lines on the graph by using these points .

Corner points of the shaded region = (0,4.33) , (8,33,0) and (7,2)

The value of P at corner points :-

`\P=4(0)+5(4.33)=21.65\P=4(8.33)+0=33.32\\P=4(7)+5(2)=38`

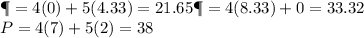
Clearly, the maximum value of P is 38 at (7,2)