Answer:
Yes, the functions intersects at the points (0,2) and (9.583,47.913).
Explanation:
We have the functions,
f of x equals one half times x squared, plus 2 i.e.
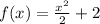 and g(x) given by the table.
and g(x) given by the table.
The general form of a linear function is y=mx+b, where m is the slope and b is the y-intercept.
We will find the slope of the function g(x),
Using
 , we get,
, we get,
i.e.
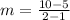
i.e.
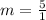
i.e. m= 5.
So, substituting (1,5) in y=5x+b ⇒ 5 = 5×1+b ⇒ b= 0.
Thus, the equation of g(x) is y= 5x.
After plotting the function f(x) and g(x), we get the following graph.
From the graph, we see that, the functions intersects at the points (0,2) and (9.583,47.913).