Answer:
Explanation:
6. The rate of change is essentially the slope. But in other words, it's how much the y changes as x increases by 1. If this rate of change is 0, that means the y-value is constant, while the x can be any real number. It can be generally given in the formula: y=b, which comes from simplifying the slope-intercept form: y=(0)x+b = b. You can also derive the same thing for a point-slope form: y-a = 0(x-b)=0 so y=a. In both cases, y is equal to some constant value. So graphing this makes a horizontal line.
7. To define a parallel line, you need the same slope, and a different y-intercept, which is under the assumption that the line has a slope that is definable. If the slope is definable, you'll have the equation: y=mx+b, where m is the same as the other line. Then you plug in the known values as x and y, to solve for b, which is the y-intercept. Now if the line is a vertical line, a parallel line can be defined as: x=a, where a doesn't equal the constant, the other vertical line is equal to. To make it pass through some point (c, d). Then you would simply set x=c, since the x is the only thing that matters, since the y-value is all real numbers, so it will eventually have the y-value d somewhere on the line.
8. To define a perpendicular line, you get the reciprocal of the slope and change the sign. So if the slope is:
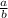 then it becomes
then it becomes
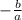 and vice versa depending on the sign. In this example, let's just say m=a/b, then the perpendicular slope would be -b/a. You can then plug this into the slope-intercept formula:
and vice versa depending on the sign. In this example, let's just say m=a/b, then the perpendicular slope would be -b/a. You can then plug this into the slope-intercept formula:
 where c is the y-intercept. Then you plug in the known point as (x, y) and solve for c, the y-intercept. Now let's say for example that you have a vertical line: x=a. In this case you can see the slope as:
where c is the y-intercept. Then you plug in the known point as (x, y) and solve for c, the y-intercept. Now let's say for example that you have a vertical line: x=a. In this case you can see the slope as:

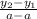 . Of course this isn't definable, but if you take the reciprocal you get something that is:
. Of course this isn't definable, but if you take the reciprocal you get something that is:
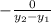 which will always evaluate to 0. This means you get a horizontal line, since the slope is 0. This means if you have a vertical line, any horizontal line should be perpendicular, which makes sense, since it should form a 90 degree angle when they intersect, because they're straight lines. To make sure that horizontal line passes through the point (b, c), you simply set the y equal to c. So y=c, will pass through (b, c), since the c is constant, and the x can equal anything so somewhere on the line it will intersect (b, c). But let's say we had a horizontal line, the reciprocal can be defined as:
which will always evaluate to 0. This means you get a horizontal line, since the slope is 0. This means if you have a vertical line, any horizontal line should be perpendicular, which makes sense, since it should form a 90 degree angle when they intersect, because they're straight lines. To make sure that horizontal line passes through the point (b, c), you simply set the y equal to c. So y=c, will pass through (b, c), since the c is constant, and the x can equal anything so somewhere on the line it will intersect (b, c). But let's say we had a horizontal line, the reciprocal can be defined as:
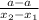 where a is the y constant. If you take the reciprocal, then you have a-a in the denominator, which gives you an undefined slope, because the perpendicular line to a horizontal line, is a vertical line. To ensure this perpendicular line passes through the point (b, c). You simply set x equal to b. so that x=b.
where a is the y constant. If you take the reciprocal, then you have a-a in the denominator, which gives you an undefined slope, because the perpendicular line to a horizontal line, is a vertical line. To ensure this perpendicular line passes through the point (b, c). You simply set x equal to b. so that x=b.