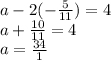The answer is (34/11, -5/11).
First, let's rewrite the 2 equations:
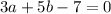

Then let's transform these 2 equations into the form ax+by=c
So that would be:
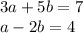
Now our goal is to isolate one of the variables a or b. Lets pick a since its easier. To do this, multiply equation 2 by -3 so that 3a + -3a=0

Now add both equations together:
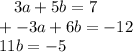
Now to isolate b, divide both sides by 11
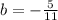
Now we know the value of b, its time to solve for a
To do this, you substitute b in any equation to -5/11. In this case, I'll choose equation 2.