Question

Special triangles 2 back

Answer 1

10. x=6√3, y=12√3

11. x=4√3, y=8√3

12. The height of the triangle is 5√3 in ≈ 8.66 in.

13. The ramp must be set 8√3 ft ≈ 13.86 ft far away from the platform.

14. The approximate total length of the path (the perimeter of the triangle)

is 42.59 m.

15. The approximate height of the tree is 4.62 m.

16. The last row of seating is 12 ft high above the ground.

Explanation:

Please, see the attached files.

Thanks.

Answer 2

Explanation:

10. From the given figure,

`(18)/(y)=sin60^(0)`

`y=(36)/(√(3))`

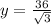
11. From the given figure,

`(12)/(y)=sin60^(0)`

`y=\frac{12{*}2}{√(3)}=(24)/(√(3))`

and
`(x)/(y)=cos60^(0)`

`x=\frac{24}{√(3){*}2}=(12)/(√(3))`

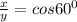
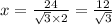
12. The sides of an equilateral triangle has length=10 inches, therefore AB=BC=AC=10

Also, AD is the height of the given triangle,then BD=DC=5

From triangle ADC,

`(AC)^(2)=(AD)^(2)+(DC)^(2)`

`100=(AD)^(2)+25`

`75=(AD)^(2)`

`AD=√(75)inches`

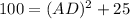
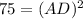
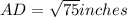
Hence, height of the triangle is
`√(75)inches`

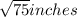
13. Height of the ramp from the ground is 8ft.

therefore, let BC=x

`(8)/(BC)=tan30^(0)`

`(8)/(x)=(1)/(√(3))`

`x=8√(3)`

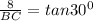
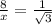
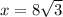
14. Let BC=x and AB=y

then,
`(x)/(18)=cos30^(0)`

`x=18{*}(√(3))/(2)=9√(3)`

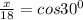
and
`(y)/(x)=tan30^(0)`

`y=9`

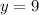
The perimeter of triangle is=Sum of all the sides=AB+BC+AC=
`9√(3)+9+18= 9√(3)+27=9(1.73)+27=42.57 inches`

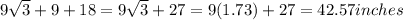
15. Let AB be the height of the tree, then

`(AB)/(8)=tan30^(0)`

`AB=8{*}(1)/(√(3))=(8)/(1.73)=4.62m`

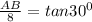
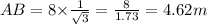
16. According to question,

`(h)/(24)=sin30^(0)`

`h=(24)/(2)=12ft`