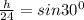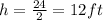Answer:
Explanation:
10. From the given figure,
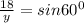
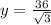
11. From the given figure,
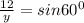
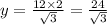
and
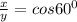
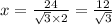
12. The sides of an equilateral triangle has length=10 inches, therefore AB=BC=AC=10
Also, AD is the height of the given triangle,then BD=DC=5
From triangle ADC,
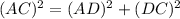
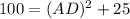
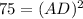
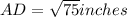
Hence, height of the triangle is
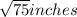
13. Height of the ramp from the ground is 8ft.
therefore, let BC=x
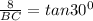
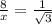
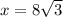
14. Let BC=x and AB=y
then,
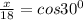
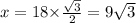
and
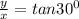
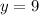
The perimeter of triangle is=Sum of all the sides=AB+BC+AC=
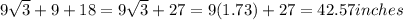
15. Let AB be the height of the tree, then
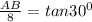
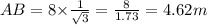
16. According to question,