Answer:

Explanation:
So generally an exponential equation is expressed in the form:
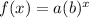 and:
and:
 . In this case we see that as x increased by 1, the y-decreases, BUT the absolute value is increasing, so it's really just reflected.
. In this case we see that as x increased by 1, the y-decreases, BUT the absolute value is increasing, so it's really just reflected.
Plug in known values:
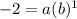

So if you think about it. you really have
-2 = a * b
-4 = a * b * b
since ab = -2, then we can substitute this into the second equation
-4 = -2 * b
-4 = -2b
Divide both sides by -2
b = 2
You can also deduce that b=2, by realizing to go from -2 to -4, you have to subtract 100% of -2 from -2. This means r=1, so b=1+1, b=2
Anyways, now it's time to solve for a, by plugging in a point as well as b.
-4 = a(2)^2
-4 = 4a
-1 = a
You can verify this by using the other point
-2 = -(2)^1
-2 = -(2)
-2 = -2
So the equation is:
