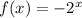Question

Write an exponential function that includes the following given pair of points.

(1,-2) and (2,-4)

Answer 1

`f(x)=-2^x`

Explanation:

So generally an exponential equation is expressed in the form:
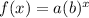`f(x)=a(b)^x` and:
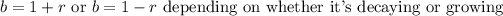`b=1+r\text{ or }b=1-r \text{ depending on whether it's decaying or growing}`. In this case we see that as x increased by 1, the y-decreases, BUT the absolute value is increasing, so it's really just reflected.

Plug in known values:

`-2=a(b)^1`

`-4=a(b)^2`

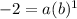
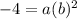
So if you think about it. you really have

-2 = a * b

-4 = a * b * b

since ab = -2, then we can substitute this into the second equation

-4 = -2 * b

-4 = -2b

Divide both sides by -2

b = 2

You can also deduce that b=2, by realizing to go from -2 to -4, you have to subtract 100% of -2 from -2. This means r=1, so b=1+1, b=2

Anyways, now it's time to solve for a, by plugging in a point as well as b.

-4 = a(2)^2

-4 = 4a

-1 = a

You can verify this by using the other point

-2 = -(2)^1

-2 = -(2)

-2 = -2

So the equation is:
`f(x)=-2^x`