Question

Solve for the variable x

Answer 1

Hello there!

Question:-

`(x-2)/3 \: = \: (x+1)/4`

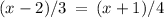
We need to find the value of x.

Solution:-

`\sf \longmapsto \: (x - 2)/(3) = (x + 2)/(4)`

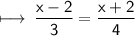
Firstly, use Cross Multiplication:-

`\sf \longmapsto \: (x - 2)*(4)=(x+1)*(3)`

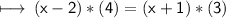
On Simplification:-

`\sf \longmapsto \: 4x - 8 = (x + 1)*3`

`\sf \longmapsto \: 4x - 8 = 3x + 3`

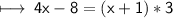
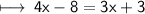
Subtract 3x from both sides :-

`\sf \longmapsto \: 4x - 8 - 3x=3x+3 - 3x`

This equation may be rewritten as :-

`\sf \longmapsto4x - 3x - 8 = 3x - 3x + 3`

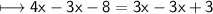
On Simplification:-

`\sf \longmapsto \: x - 8 = 0x + 3`

`\sf \longmapsto \: x - 8 = 3`

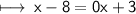
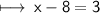
Add 8 to both sides:-

`\sf \longmapsto \: x - 8 + 8 = 3 + 8`

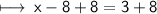
As (-)and (+) equals to (-),

`\sf \longmapsto \: x - 0 = 11`

`\: \sf \longmapsto \: x = 11`

______________________________________

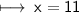
Henceforth, the value of x is :-

`\boxed{\huge\tt x = 11}`

______________________________________

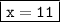
Please let me know if you have any questions.

~MisterBrian

Answer 2

Given fractional expression:

`{\sf \longmapsto (x-2)/(3) = (x+1)/(4)}`

Cross multiply the numbers.

`{\sf \longmapsto 4 (x-2) = 3 (x +1)}`

Multiply the number outside the bracket with the numbers in the bracket.

`{\sf \longmapsto 4x - 8 = 3x +3}`

Shift all variables on LHS and constants on RHS.

`{\sf \longmapsto 4x - 3x = 3+8}`

Subtract the values on LHS and Add the values on RHS.

`{\sf \longmapsto 7x = (11)}`

Shift the number 7 from LHS to RHS.

`{\sf \longmapsto x = (11)/(7)}`

`\underline{\boxed{\bf So, \: the \: value \: of \: x \: is \: (11)/(7).}}`

Verification :

`{\sf \longmapsto (x-2)/(3) = (x+1)/(4)}`

Substitute the value of the x.

`{\sf \longmapsto ((11)/(7)-2)/(3)= ((11)/(7)+1)/(4)}`

`{\sf \longmapsto ((11-14)/(7))/(3) = ((11+7)/(7))/(4)}`

`{\sf \longmapsto ((-3)/(7))/(3)= ((18)/(7))/(4)}`

Cancel the number 7 on numerator Of LHS and RHS.

`{\sf \longmapsto (-3)/(3) = (18)/(4)}`

Write the fraction in lowest form by cancellation method.

`{\sf \longmapsto (-3)/(3) = (9)/(2)}`

So,

`{\sf \longmapsto LHS ≠ RHS}`