Answer:
3√2
Explanation:
We have to find distance between two points.
We represent a+bi as (a,b) on graph.
Hence, 5-2i can be represented as (5,-2).
and 8+i can be represented as (8,1).
By using distance formula, we can find distance between two points.
d=

d=
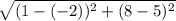
d=
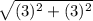
d=
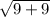
d=
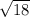
d=
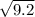
d=3√2 is distance between (5-2i) and (8+i).