Question

What is the distance between (5 - 2i) and (8 + i)?

Answer 1

3√2

Explanation:

We have to find distance between two points.

We represent a+bi as (a,b) on graph.

Hence, 5-2i can be represented as (5,-2).

and 8+i can be represented as (8,1).

By using distance formula, we can find distance between two points.

d=
`\sqrt{(y_(2)-y_(1) )^(2) +(x_(2) -x_(1) )^(2)}`

d=
`\sqrt{(1-(-2))^(2)+(8-5)^(2)}`

d=
`\sqrt{(3)^(2) +(3)^(2) }`

d=
`√(9+9)`

d=
`√(18)`

d=
`√(9.2)`

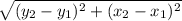
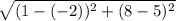
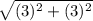
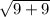
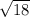
d=3√2 is distance between (5-2i) and (8+i).

Answer 2

Explanation:

In complex plane we can see a+bi as the point (a,b).

so 5-2i can be seen as (5,-2)

and 8+i can be seen as (8,1)

Now we can use the distance formula to find the distance between the two points .

Distance formula is

`D=√((x1-x2)^2+(y1-y2)^2)`

Plugging the respective values we get

`D= √(((5-8)^2+(-2-1)^2)\\D= \sqrt{(-3)^2+(-3)^2\\`

`D = √(9+9) \\D=√(18) \\D=3√(2)`

so Distance is
`3√(2)`