Answer:
Statement 2.: QK/KL=16/40; PK/MK=26/65
Statement 3.: QK/KL=2/5=PK/MK
Reason 4: Vertical angles
Reason 5: SAS
Explanation:
Statement 2:
The smaller of the sides adjacent to <PKQ (QK=16) in triangle PKQ is corresponding with the smaller of the sides adjacent to <MKL (KL=40) in triangle MKL.
The larger of the sides adjacent to <PKQ (PK=26) in triangle PKQ is corresponding with the larger of the sides adjacent to <MKL (MK=65) in triangle MKL.
Ratio of the corresponding sides:
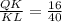
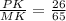
Statement 3. Simplifying ratios:
Dividing the numerator and denominator by 8:
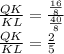
Dividing the numerator and denominator by 13:
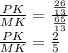
Reason 4: <MKL is conguent with <PKQ because they are vertical angles (angles opposite by the vertex)
Reason 5: The two triangles (∆QPK y ∆LMK) have a congruent angle (<MKL with <PKQ) and the corresponding sides including this angle proportionals (QK/KL=2/5=PK/MK), then the two triangles (∆QPK y ∆LMK) are similar. This case is SAS.