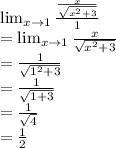Question

Evaluate the limit as x approaches 1 of the ((square root of the quantity x squared plus 3 ) minus 2) all over x minus 1. Show work

Answer 1

`\lim_(x \to 1)\frac{\sqrt{x^(2)+3 }-2}{{x-1}}=(1)/(2)`

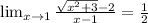
Explanation:

`\lim_(x \to 1)\frac{\sqrt{x^(2)+3 }-2}{{x-1}}`

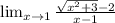
if we put x = 1 directly in the epression above we will get an indeterminate form
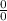`(0)/(0)`, so instead we will use L’Hospital's Rule.

Take derivative of numerator and denominator separately and then apply the limit.

`(d)/(d(x))\sqrt{x^(2)+3 }-2 = \frac{x}{\sqrt{x^(2)+3 } }\\(d)/(d(x)) (x-1) = 1\\`

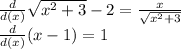
So now the expression becomes: By puttin x = 1 in the expression now we can find the solution

`\lim_(x \to 1) \frac{\frac{x}{\sqrt{x^(2)+3 } }}{1}\\=\lim_(x \to 1)\frac{x}{\sqrt{x^(2)+3 }}\\=\frac{1}{\sqrt{1^(2)+3 }}\\=(1)/(√(1+3 ))\\=(1)/(√(4 ))\\=(1)/(2)`