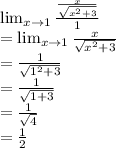Answer:
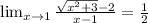
Explanation:
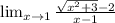
if we put x = 1 directly in the epression above we will get an indeterminate form
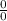 , so instead we will use L’Hospital's Rule.
, so instead we will use L’Hospital's Rule.
Take derivative of numerator and denominator separately and then apply the limit.

So now the expression becomes: By puttin x = 1 in the expression now we can find the solution