Answer:
Option D. (5,4)
Explanation:
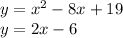
Using the method of equaling the two equations:
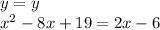
This is a quadratic equation, then we must equal to zero. Equaling to zero subtracting 2x and adding 6 to both sides of the equation:
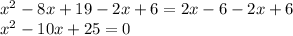
Factoring:
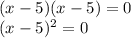
Solving for x: Square root both sides of the equation:

Adding 5 to both sides of the equation:
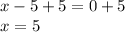
Replacing x=5 in any of the two given equations:
y=2x-6
y=2(5)-6
y=10-6
y=4
Solution: x=5 and y=4: Point=(x,y)→Point=(5,4)