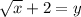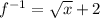Question

Restrict the domain of the function f(x)=(x-2)to the power of 2 so it has an inverse. Then determine its inverse function.

Answer 1

restriction of domain is x>=2

`f^(-1)=√(x)+2`

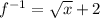
Explanation:

Restrict the domain of the function
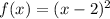`f(x)=(x-2)^2` so it has an inverse

To restrict the domain we find the vertex

VErtex form of the equation is

`y=(x-h)^2+k` vertex is (h,k). restriction of domain is x>=h

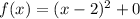`f(x)=(x-2)^2+0` , vertex is (2,0)

So restriction of domain is x>=2

now we find inverse function

`f(x)=(x-2)^2`

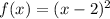
Replace f(x) with y

`y=(x-2)^2`

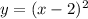
Replace x with y and y with x

`x=(y-2)^2`

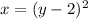
To remove square we take square root on both sides

`√(x) =y-2`

Add 2 on both sides

`√(x)+2 =y`

`f^(-1)=√(x)+2`

Answer 2

Explanation:

Given is a function

`f(x) =(x-2)^2`

This function is a parabola with vertex at (2,0) and axis of symmetry is x=2

Hence for x<2 the curve would be reflection of x>2

To get inverse we must get one to one funciton only.

So restrict the domain of f(x) to
`[2,∞)`

Then we have f(x) as one to one with domain x≥2 and range is R+

`f^(-1) (x)=+√(x) +2`

For this inverse domain is R+ and range is
`[2,∞)`