Answer: 0.625 m
Step-by-step explanation:
Given:
Final velocity of the car = 3.5 m/s
While the car rolls down the hill, there is a conversion of potential energy (PE) to kinetic energy (KE). Therefore, applying the conversion of energy as,
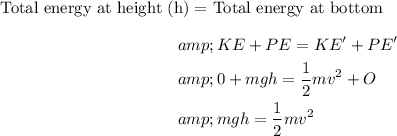
Here, m denotes the mass of the car, g is the gravitational acceleration, having a value of 9.8 m/s^2. And h is the height of the hill.
Solving for h,
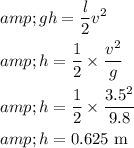
Therefore, the required height of hill is 0.625 m