Answer:
1. Translated left 5 units
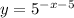
2. Translated right by 5 units
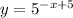
3. Translated up by 5 units
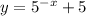
4. Translated down by 5 units
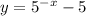
5. Reflected across the x-axis

6. Reflected across the y-axis

Explanation:
The given parent function is
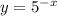
The transformation of this function is defined as
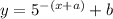
Where, a represents horizontal shift and b represents vertical shift.
If a>0, then graph shifts a units left and if a<0, then graph shifts a units right.
If b>0, then graph shifts b units up and if b<0, then graph shifts b units down.
1. Translated left 5 units
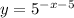
2. Translated right by 5 units
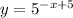
3. Translated up by 5 units
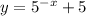
4. Translated down by 5 units
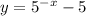
5. If graph reflected across the x-axis, then the graph passes through (x,-y).


6. If graph reflected across the y-axis, then the graph passes through (-x,y).


Therefore the required matching is
1. Translated left 5 units
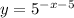
2. Translated right by 5 units
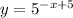
3. Translated up by 5 units
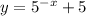
4. Translated down by 5 units
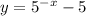
5. Reflected across the x-axis

6. Reflected across the y-axis
