Answer:
Inequality:
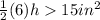
Solve for 'h': h > 5 in.
Explanation:
The formula for the area of a triangle is: area =
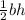 , where 'b'=the length of the base and 'h' = the height. Since the area of the sign must be more than 15 in², the inequality must be '> 15 in²'.
, where 'b'=the length of the base and 'h' = the height. Since the area of the sign must be more than 15 in², the inequality must be '> 15 in²'.
Using the formula for area and the given values, we can set up the following inequality:
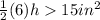
Solving for 'h', we can first multiply both sides by
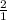 :
:
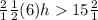
Divide both sides by 6: 6h/6 > 30/6
Solve for h: h > 5in